Allgemeines zum KV-Diagramm
Das KV-Diagramm (KV steht hierbei für Karnaugh-Veitch) wurde 1952 von Edward W. Veitch entwickelt und 1953 von Maurice Karnaugh optimiert.
Ein KV-Diagramm dient hauptsächlich der Vereinfachung, aber auch der übersichtlichen Veranschaulichung von booleschen Funktionen. Eine disjunktive Normalform lässt sich somit meist zu einem komplett minimalen logischen Ausdruck umformen. Falls der Ausdruck noch nicht minimal ist, kann eine weitere Vereinfachung durch Anwenden der booleschen Rechenregeln vollbracht werden.
Bei n Eingangsvariablen hat ein KV-Diagramm 2n Felder, weshalb dieses Verfahren nur bei Schaltfunktionen mit bis zu 4 Eingängen sinnvoll ist. Es ist außerdem an den Rändern mit den Variablen beschriftet, wobei jede Variable in negierter- und nicht-negierter Form vorkommt.
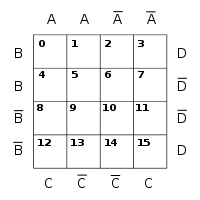
Ein möglicher Aufbau kann zum Beispiel so aussehen:
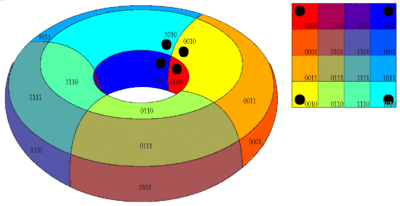
Oft wird auch eine Torus-Form verwendet. Diese hat den Vorteil, dass das Zusammenfassen an den Kanten/Ecken einfacher verläuft: